The Pigeonhole Principle and Ramsey's Theorem
Introduction
Picture the scene. You are in a small village, and there are 7 pigeons on the island. Of course, they are enjoying their time in the village (it seems), but how about when the sun relegates itself below the sea and the sands: when the stars come out?
There are some pigeonholes on the ground for them to rest and protect themselves so they don't become a midnight snack - upon further inspection, however, you find there is only 6. The soil is too rough for you to create another one, so, naturally, what happens?
Two pigeons enter one pigeonhole. Of course - but what does this have to do with maths?
Enter the pigeonhole principle.
What is the pigeonhole principle?
If you weren't caught up in trying to find a loophole to the analogy I had laid out, you'll find the pigeonhole principle really helps - the pigeonhole principle is a theorem used in mathematical fields like data science, discrete maths, and combinatorics.
Essentially, it that states that if you organise n items into m containers, and n > m... at least one container will hold two or more of these items.
It stems from basic combinatorics and replacement probability (and maybe common sense); however, it goes a lot deeper than what meets the eye in its applications, which to me is what makes it so elegant.
A proof by contradiction of the pigeonhole principle
The pigeonhole principle is quite simple to wrap your head around conceptually, which might coax you into thinking the proof will be something as diabolical as trying to defend Jack the Ripper in a court of law...
...but it assuredly isn't. Imagine that you are given that there are n items and m containers, and n>m.
If the pigeonhole principle was false, then at most there would be 1 item per container.
This would mean there are m items and m containers, which implies n=m.
However, this contradicts what was given!
As a result, the pigeonhole principle is a FACT.
1. Unwishful thinking
The point of the pigeonhole principle in a lot of its applications is that you have to imagine what happens given the worst possible luck in trying to make it happen.
That may not make sense at first, but imagine you have a deck of cards (INCLUDING joker cards) and you'd like at least two cards of the same suit.
The question is: how many cards need to be drawn from the top of the deck to GUARANTEE success?
HINT: someone has rigged the shuffling of these cards such that it is really hard to achieve this. What would they do?
Click for solution
If someone else was to rig the cards to make it as hard to achieve your goal as possible, they would maximise the amount of cards you have to draw, which would require you to exhaust every single suit, including the joker.
So imagine... heart, spade, club, diamond, joker... what comes next?
The fact is, it doesn't matter - we know the next card is going to be one of these, so the answer is 6.
2. Application to geometry
Let's now think about something a little more abstract than a deck of cards.
Suppose you have a 1cm by 1cm square and you have to pick 5 points on the square... how do you know the maximum distance between the closest pair of points will be sqrt(2)/2 cm?
Click for solution
Think unwishfully again - maximise the distance with the first 4 points by making sure they're all as far as can be (i.e. on the corners of the square.
Now you need one more point. There's two ways this could go down...
1. You place the fifth point in the middle and the corner points alongside the centre point make 4 pairs each which are all the joint closest pair. Their distance, according to the Pythagorean theorem, IS sqrt(2)/2 cm, so the rule holds.
2. Imagine the same scenario except the point is moved around. This increases the distance between some pairs but also DECREASES some such that the distance is LESS than this, so again, the rule holds!A slight extension
We can go a bit further with this... if r is the average number of items in a container, one item will assuredly have a MINIMUM of ceil(n/r) where ceil() rounds up any decimal to the first integer above it e.g. 2.46 goes to 3, 5.55 goes to 6, etc.
You can prove this a similar way... but I'll leave this one to you.
3. Ramsey's "Friends and Strangers" Theorem
This is based on a theorem by Frank Ramsey, a mathematician who studied maths at Trinity College, Cambridge: throughout his studies, he had done a fair bit on combinatorics and graph theory.
Now let's suppose you have a room of people who are either friends or, well, not friends - we don't really care why. The question is, how many people do we need in this room to ascertain that there are three people who ARE friends or three who AREN'T?
Click for solution
The images here show a diagrammatic solution to this problem - the answer is 6.
It's a lot deeper than that, though: have a look. Hopefully you understand it given your prior knowledge of the pigeonhole principle :-)
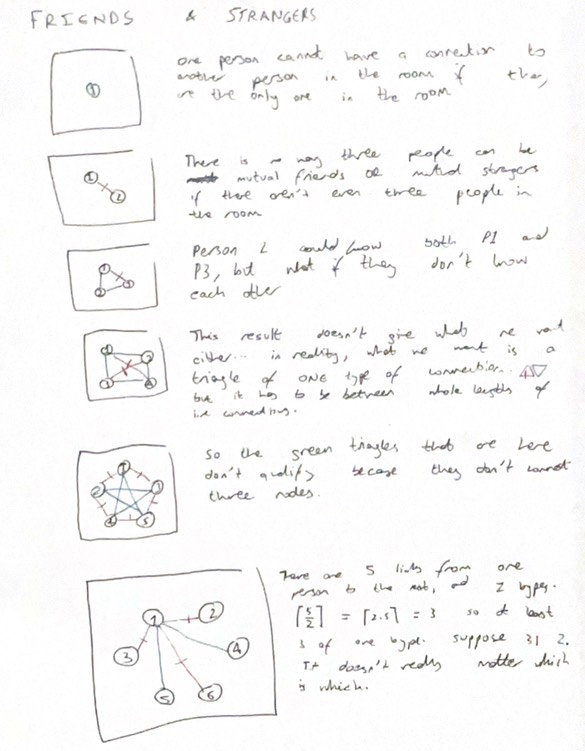
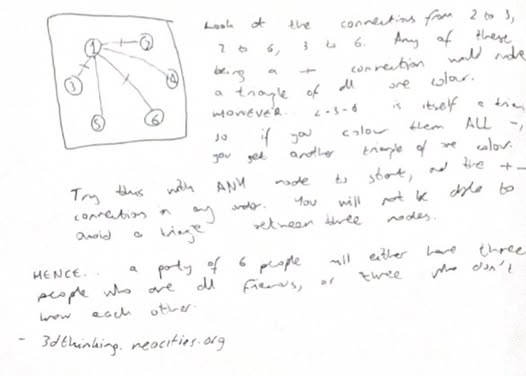
See how we used the pigeonhole principle here? This is why I love the pigeonhole principle; no-one thinks about it when seeing how many mutual friends they have with their own on social media and yet still it ever so discreetly (heh...) rears its head at us for someone like me (or you, if you're reading this) to point out.4. Four friendly faces
I like to play this one video game called Balatro sometimes- it's quite a fun play, especially for those who love to use maths to model (or overthink) real-life situations.
Its card system works such that you pick up five cards and try to score as high as you can with them, but you have to be careful in what you do when playing it; getting four cards of the same suit accrues more points than only getting, say, three of the same suit.
The game throws some curveballs at you, though. Sometimes they'll invalidate all cards of a specific suit. Sometimes they'll force you only to play one hand. The interesting case here, however, is when they hide all of your face cards.
The question is, if you have a bunch of really crummy cards but you at least have four face cards (and you know all 12 of your face cards haven't been destroyed, which you CAN let happen in the game for those who haven't played it), how likely is a four-in-a-row with these cards?
You are given that the cards are sorted highest to lowest (e.g. KQQJ is OK but not KQJQ) as the game does facilitate this by default if that's what you want.
Click for solution
Well, we know as per the pigeonhole principle that a pair can be ascertained if you only pick the four hidden cards.
You could simply deduce what kind of combinations you could get and find your answer based on that, but it would probably be more elegant to use some nifty combinatorics.
If you imagine that two random pointers separate the four cards into three different groups, you can start to think of all the different positions the pointers could hold. Two pointers + four cards = six items. Two will be the pointer. 6C2 = 15. There are 15 different combinations.
From this point, it should be understood that you can have K*4, Q*4, or J*4 as your four face cards. 3/15 = 0.2, so there is a 0.2 probability. This is better than a dice roll! For those who play the game, or those who are interested, this is a good way to hedge bets.
5. Application to hashing
Hashes in computer science and cryptography are used to verify that data is correct without directly comparing the data. For example, the value 1234576 might be hashed with a function involving the value, a simple example being the sum of all its digits, which is 28. Hashing can be used to confirm with a simple test that it's all smooth sailing...
One reason for this is for security purposes - for example, any system you need to make an online account for will indubitably (God willing) use hashing, because there is no good reason for that stuff to just be kicking about on a database.
Another reason which is perhaps less considered is the amount of time it saves for things that are perhaps longer than passwords...like software on a software distribution console or platform. Think gaming. Think the Xbox, the PlayStation, the Switch, the Steam Deck...and yes, there's examples outside of gaming, ones that don't pertain to clicking cards/shooting opponents/cruising through fictional streets or what-have-you, but this one is probably the easiest to explain.
...because regardless of how much of a "hardcore gamer" you may claim to be, it's unlikely that you'll want to sift through gigabytes of data each time you want to make sure your device hasn't scuppered you by playing about with the files on them.
For that reason, there is a "hash" which is a LOT smaller than the original file size.
This should be completely fine, right?
...right?
Click for solution
Think about it in terms of what files actually are - a sequence of 0s and 1s. With some basic combinatorics, or perhaps from your own stock knowledge, you'll clock that there's an exponential relationship of base 2 between the number of bits and the number of possible files.
Since the original file is logically far larger than the hash, there are going to be WAY more files than hash values; the pigeonhole principle now has it that there'll be some with the exact same hash, and probably a lot more than just two. It'll be 2^(x-y) where x is the amount of bits in size your game is, and y for the hash size... there is NO reason that y should even be 10% of what x is. That means there's a hell of a lot of files sharing a hash... and that's bad... because now your gaming console thinks you'll be fine to load a game you assuredly WON'T be fine loading... and that's bad... because that could jam up your game progress... and that's bad... because you may well have spent more hours than you should on that game of yours. Yeesh.
Thankfully, strong hash functions will be designed to make these "hash collisions" as they are called unlikely, and yes, sure, this problem is inevitable, but equally, I don't see you preparing for when your computer gets obliterated by a brash, indifferent bolt of lightning, and it begs the question: what does the pigeonhole principle have to say about lightning striking twice in the same place?
The end
I suppose this marks the end of this article. I hope you enjoyed! :)
3Dthinking: think about maths from a new perspective | main menu

